graphics-snippets

StackOverflow

Matrix definitions and operations

Matrix definitions

3*3 matrix

A 3*3 matrix looks like this:

  c0  c1  c2             x   y   z
[ Xx  Yx  Zx ]        [  0   4   8 ]
[ Xy  Yy  Zy ]        [  1   5   9 ]
[ Xz  Yz  Zz ]        [  2   6  10 ]

And the memory image of a 3*3 matrix like this:

[ Xx, Xy, Xz, Yx, Yy, Yz, Zx, Zy, Zz, Tx, Ty, Tz ]

Initializing a mat3 m33 in GLSL:

mat3 m33 = mat3(
    vec3( Xx, Xy, Xz ),
    vec3( Yx, Xy, Yz ),
    vec3( Zx  Zy  Zz ),
    vec3( Tx, Ty, Tz ) );

Addressing the columns of a mat3 m33; in GLSL:

vec3 x = m33[0].xyz;
vec3 y = m33[1].xyz;
vec3 z = m33[2].xyz;

4*4 matrix

A “mathematical” 4*4 matrix looks like this:

  c0  c1  c2  c3            c0  c1  c2  c3
[ Xx  Yx  Zx  Tx ]        [  0   4   8  12 ]
[ Xy  Yy  Zy  Ty ]        [  1   5   9  13 ]
[ Xz  Yz  Zz  Tz ]        [  2   6  10  14 ]
[  0   0   0   1 ]        [  3   7  11  15 ]

But the memory image of a 4*4 OpenGL matrix looks like this:

[ Xx, Xy, Xz, 0, Yx, Yy, Yz, 0, Zx, Zy, Zz, 0, Tx, Ty, Tz, 1 ]

Initializing a mat4 m44 in GLSL:

mat4 m44 = mat4(
    vec4( Xx, Xy, Xz, 0.0),
    vec4( Yx, Xy, Yz, 0.0),
    vec4( Zx  Zy  Zz, 0.0),
    vec4( Tx, Ty, Tz, 1.0) );

Addressing the columns of a mat4 m44; in GLSL:

vec4 c0 = m44[0].xyzw;
vec4 c1 = m44[1].xyzw;
vec4 c2 = m44[2].xyzw;
vec4 c3 = m44[3].xyzw;

Column-major order

See The OpenGL Shading Language 4.6, 5.4.2 Vector and Matrix Constructors, page 108
and OpenGL ES Shading Language 3.20 Specification, 5.4.2 Vector and Matrix Constructors, page 110:

To initialize a matrix by specifying vectors or scalars, the components are assigned to the matrix elements in column-major order .

mat4(float, float, float, float,  // first column
     float, float, float, float,  // second column
     float, float, float, float,  // third column
     float, float, float, float); // fourth column

Note, in compare to a mathematical matrix where the columns are written from top to bottom, which feels natural, at the initialization of an OpenGL matrix, the columns are written from the left to the right. This leads to the benefit, that the x, y, z components of an axis or of the translation are in direct succession in the memory. This is a big advantage when accessing the axis vectors or the translation vector of the matrix.
See also Data Type (GLSL) - Matrix constructors.


See further:


<hr/>

Fixed Function pipeline matrix stack


Noice, that the Fixed Function Pipeline is deprecated. See also Khronos wiki - Legacy OpenGL.


In OpenGL there is one matrix stack for each matrix mode (See glMatrixMode). The matrix modes are GL_MODELVIEW, GL_PROJECTION, and GL_TEXTURE.

Multiplication: See the documentation of glMultMatrix:

glMultMatrix multiplies the current matrix with the one specified using m, and replaces the current matrix with the product.

Translation: See the documentation of glTranslate:

glTranslate produces a translation by x y z . The current matrix (see glMatrixMode) is multiplied by this translation matrix, with the product replacing the current matrix.

Rotation: See the documentation of glRotate:

glRotate produces a rotation of angle degrees around the vector x y z . The current matrix (see glMatrixMode) is multiplied by a rotation matrix with the product replacing the current matrix.

Scaling: See the documentation of glScale:

glScaleproduces a nonuniform scaling along the x, y, and z axes. The three parameters indicate the desired scale factor along each of the three axes. The current matrix (see glMatrixMode) is multiplied by this scale matrix.


Matrix stack

To imagine how the matrix operations change the model, the operations onto the matrix stack have to be “read” in the reversed order. This is, because the current matrix of the matrix stack is multiplied by the matrix which is specified by the new operation and the matrices are stored in column-major order.

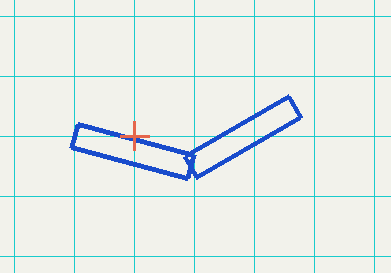
Example of a robot arm from OpenGL Programming Guide - Chapter 3 Viewing - Building an Articulated Robot Arm.
See also OpenGL translation before and after a rotation.

float shoulder_ang_deg = -15.0f;
float elbow_ang_deg    =  45.0f;

glTranslatef(-1.0f, 0.0f, 0.0f);
glRotatef(shoulder_ang_deg, 0.0f, 0.0f, 1.0f);
glTranslatef(1.0f, 0.0f, 0.0f);
glPushMatrix();
glScalef(2.0f, 0.4f, 1.0f);
glutWireCube(1.0f);
glPopMatrix();    

glTranslatef(1.0f, 0.0f, 0.0f);
glRotatef(elbow_ang_deg, 0.0f, 0.0f, 1.0f);
glTranslatef(1.0f, 0.0f, 0.0f);
glPushMatrix();
glScalef(2.0f, 0.4f, 1.0f);
glutWireCube(1.0f);
glPopMatrix();

Explanation:

Start with the elbow cube

glutWireCube(1.0f);

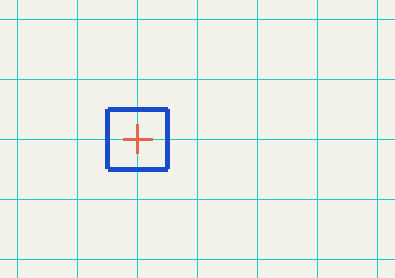
arm_01

Scale the elbow

glPushMatrix();
glScalef(2.0f, 0.4f, 1.0f);
glutWireCube(1.0f);
glPopMatrix();

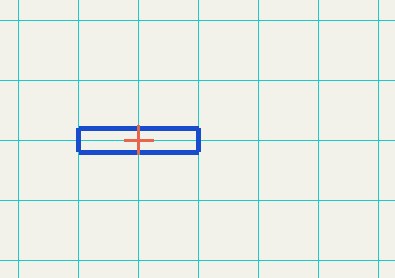
arm_02

Move it to the right

glTranslatef(1.0f, 0.0f, 0.0f);

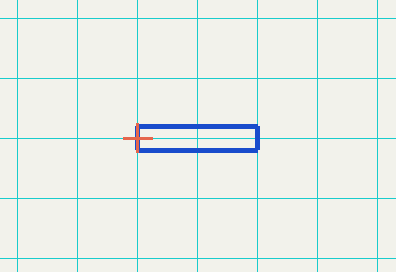
arm_03

Rotate the elbow

glRotatef(45.0f, 0.0f, 0.0f, 1.0f);

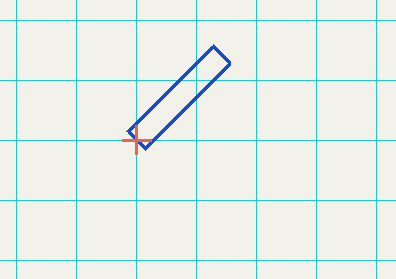
arm_04

Move the rotated elbow to the right

glTranslatef(1.0f, 0.0f, 0.0f);

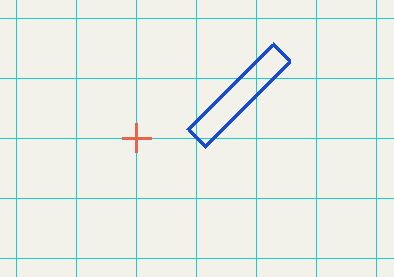
arm_05

Draw the sholder cube

glutWireCube(1.0f);

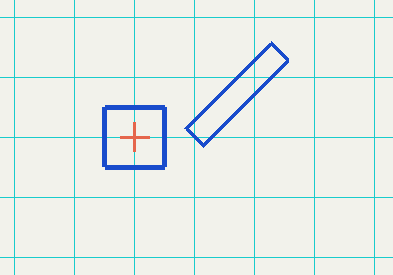
arm_06

Scale the sholder

glPushMatrix();
glScalef(2.0f, 0.4f, 1.0f);
glutWireCube(1.0f);
glPopMatrix();

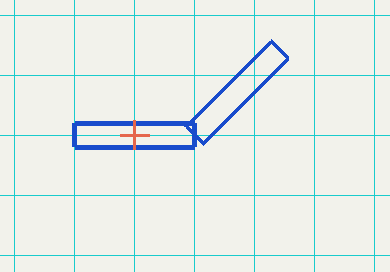
arm_07

Move the arm (elbow and shoulder) to the right

glTranslatef(1.0f, 0.0f, 0.0f);

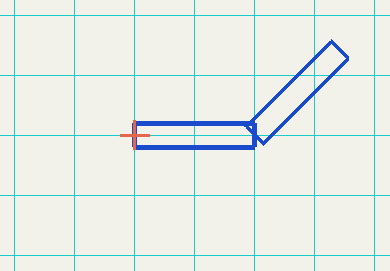
arm_08

Rotate the arm

glRotatef(-15.0f, 0.0f, 0.0f, 1.0f);

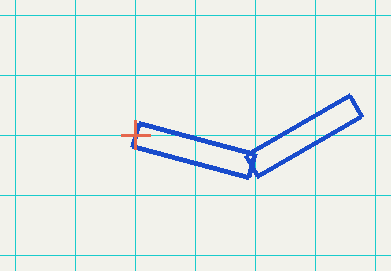
arm_09

Move the arm to its final position (to the left)

glTranslatef(-1.0f, 0.0f, 0.0f);

arm_10

Matrix stack and Shader

In GLSL (1.10) there are provided a bunch of Built-In Uniforms. See OpenGL Shading Language 1.10 Specification; 7.5 Built-In Uniform State; page 45.
One of them is gl_ModelViewProjectionMatrix of type mat4, which provides the transformation by the model view and projection matrix. Separated gl_ModelViewMatrix and gl_ProjectionMatrix exists as well.

To use them, it has to be switch down the GLSL version in the fragment shader. It is sufficient to change the version in the vertex shader, it would be possible to use a different (higher) version in the fragment shader. Of course this won’t be possible with a core profile context, but the fixed function matrix stack can’t be use in the core profile, too:

#version 120

void main()
{
    gl_Position = gl_ModelViewProjectionMatrix * gl_Vertex;
}

A handy function is ftransform, which is described in OpenGL Shading Language 1.10 Specification; 8.4 Geometric Functions; page 54:

For vertex shaders only. This function will ensure that the incoming vertex value will be transformed in a way that produces exactly the same result as would be produced by OpenGL’s fixed functionality transform. It is intended to be used to compute gl_Position, e.g.,

gl_Position = ftransform();

This function should be used, for example, when an application is rendering the same geometry in separate passes, and one pass uses the fixed functionality path to render and another pass uses programmable shaders.


<hr/>

Matrix operations

Matrix translation

C++:

void Translate( GLfloat m[], GLfloat x, GLfloat y, GLfloat z )
{
    float translation[]{
        1.0f, 0.0f, 0.0f, 0.0f,
        0.0f, 1.0f, 0.0f, 0.0f,
        0.0f, 0.0f, 1.0f, 0.0f,
        x,    y,    z,    1.0f };

    multiplyMatrix(&m[0], translation, &m[0]);
}

Python:

def Translate(matA, trans):
    matB = numpy.copy(matA)
    for i in range(0, 4): matB[3,i] = matA[0,i] * trans[0] + matA[1,i] * trans[1] + matA[2,i] * trans[2] + matA[3,i] 
    return matB

Note, this would be what glm::translate does.

glm::mat4 translation = glm::translate(glm::mat4(), glm::vec3(0.5f, 0.0f, 0.0f));

Matrix rotation

C++:

void Rotate( GLfloat m[], GLfloat angle, GLfloat x, GLfloat y, GLfloat z )
{
    float radians = angle * M_PI/180;
    float c = cos(radians);
    float s = sin(radians);

    float rotation[16]{
        x*x*(1.0f-c)+c,   x*y*(1.0f-c)-z*s, x*z*(1.0f-c)+y*s, 0.0f,
        y*x*(1.0f-c)+z*s, y*y*(1.0f-c)+c,   y*z*(1.0f-c)-x*s, 0.0f,
        z*x*(1.0f-c)-y*s, z*y*(1.0f-c)+x*s, z*z*(1.0f-c)+c,   0.0f,
        0.0f,             0.0f,             0.0f,             1.0f };

    multiplyMatrix(&m[0], rotation, &m[0]);
}

Python:

def Rotate(matA, angRad, axis):
    matB = numpy.copy(matA)
    s, c = math.sin(angRad), math.cos(angRad)
    x, y, z = axis[0], axis[1], axis[2] 
    return numpy.matrix( [
        [x*x*(1-c)+c,   x*y*(1-c)-z*s, x*z*(1-c)+y*s, 0],
        [y*x*(1-c)+z*s, y*y*(1-c)+c,   y*z*(1-c)-x*s, 0],
        [z*x*(1-c)-y*s, z*y*(1-c)+x*s, z*z*(1-c)+c,   0],
        [0,             0,             0,             1] ] )

Note, this would be what glm::rotate does.

glm::mat4 rotation = glm::rotate(glm::mat4(), angRad, glm::vec3(1.0f, 0.0f, 0.0f));

Matrix scaling

C++:

void Scalef( GLfloat m[], GLfloat x, GLfloat y, GLfloat z )
{
    float scaling[]{
        x,    0.0f, 0.0f, 0.0f,
        0.0f, y,    0.0f, 0.0f,
        0.0f, 0.0f, z,    0.0f,
        0.0f, 0.0f, 0.0f, 1.0f };

    multiplyMatrix(&m[0], scaling, &m[0]);
}

Python:

def Scale(matA, s):
    matB = numpy.copy(matA)
    for i0 in range(0, 3):
        for i1 in range(0, 4): matB[i0,i1] = matA[i0,i1] * s[i0] 
    return matB

Note, this would be what glm::scale does.

glm::mat4 scaling = glm::scale(glm::mat4(), glm::vec3(1.0f, 2.0f, 1.0f));

Reset the scale of a 4x4 matrix

Knowing the matrix, you can calculate the scale for each axis. In the following m is the matrix:

float scaleX = sqrt(m[0][0]*m[0][0] + m[0][1]*m[0][1] + m[0][2]*m[0][2]);
float scaleY = sqrt(m[1][0]*m[1][0] + m[1][1]*m[1][1] + m[1][2]*m[1][2]);
float scaleZ = sqrt(m[2][0]*m[2][0] + m[2][1]*m[2][1] + m[2][2]*m[2][2]);

If you want to “reset” the scale while keeping the absolute translation and rotation, you need to normalize the axis. The length of a normalized vector (Unit vector) is 1:

for (int i = 0; i < 3; ++i)
{
    m[0][i] /= scaleX;
    m[1][i] /= scaleY;
    m[2][i] /= scaleZ;
}

If the scale for the 3-axes is identical, the result for scaleX, scaleY, scaleZ will also be identically. Hence, you can tweak the code and only calculate one scale.

Matrix multiplication (concatenation)

See also OpenGL Shading Language 4.60 Specification (HTML) - 5.10. Vector and Matrix Operations.

OpenGL matrices are stored in colum major order. Multiplying the matrix M with the matrix N means multiplying the columns of matrix M with the rows of matrix N and storing the result to the columns of the target.

A matrix multiplication C = A * B works like this:

Matrix4x4 A, B, C;

// C = A * B
for ( int k = 0; k < 4; ++ k )
    for ( int j = 0; j < 4; ++ j )
        C[k][j] = A[0][j] * B[k][0] + A[1][j] * B[k][1] + A[2][j] * B[k][2] +  A[3][j] * B[k][3];

C++:

void multiplyMatrix( float A[], float B[], float P[] )
{
    float C[16];
    for ( int k = 0; k < 4; ++ k ) {
        for ( int j = 0; j < 4; ++ j ) {
            C[k*4+j] =
                A[0*4+j] * B[k*4+0] +
                A[1*4+j] * B[k*4+1] +
                A[2*4+j] * B[k*4+2] +
                A[3*4+j] * B[k*4+3];
        }
    }
    std::copy(C, C+16, P);
}

Python:

def Multiply(matA, matB):
    matC = numpy.copy(matA)
    for i0 in range(0, 4):
        for i1 in range(0, 4):
            matC[i0,i1] = matB[i0,0] * matA[0,i1] + matB[i0,1] * matA[1,i1] + matB[i0,2] * matA[2,i1] + matB[i0,3] * matA[3,i1]
    return matC

def m3dMultiply(A, B):
    C = (GLfloat * 16)(*identityMatrix)
    for k in range(0, 4):
        for j in range(0, 4):
            C[k*4+j] = A[0*4+j] * B[k*4+0] + A[1*4+j] * B[k*4+1] + \
                       A[2*4+j] * B[k*4+2] + A[3*4+j] * B[k*4+3]
    return C

def m3dMultiply(A, B):
    C = (GLfloat * 16)(*identityMatrix)
    for k in range(0, 4):
        for j in range(0, 4):
            C[k*4+j] = sum([A[i*4+j] * B[k*4+i] for i in range(0, 4)])
    return C

A concatenation of 2 matrices (matrix multiplication) is not commutative:
e.g. multiplication of a translation matrix and a rotation matrix around the Y-axis

The translation matrix looks like this:

Matrix4x4 translate

translate[0] : ( 1,  0,  0,  0 )
translate[1] : ( 0,  1,  0,  0 )
translate[2] : ( 0,  0,  1,  0 )
translate[3] : ( tx, ty, tz, 1 )

And the rotation matrix around Y-Axis looks like this:

Matrix4x4  rotate;
float      angle;

rotate[0] : ( cos(angle),  0, sin(angle), 0 )
rotate[1] : ( 0,           1, 0,          0 )
rotate[2] : ( -sin(angle), 0, cos(angle), 0 )
rotate[3] : ( 0,           0, 0,          1 )


The result of translate * rotate is this:

model[0] : ( cos(angle),  0,  sin(angle), 0 )
model[1] : ( 0,           1,  0,          0 )
model[2] : ( -sin(angle), 0,  cos(angle), 0 )
model[3] : ( tx,          ty, tz,         1 )

translate * rotate


Note, the result of rotate * translate would be:

model[0] : ( cos(angle),                     0,   sin(angle),                     0 )
model[1] : ( 0,                              1,   0,                              0 )
model[2] : ( -sin(angle),                    0,   cos(angle),                     0 )
model[3] : ( cos(angle)*tx - sin(angle)*tx,  ty,  sin(angle)*tz + cos(angle)*tz,  1 )

rotate * translate


See further:


<hr/>

Transposed matrix

The transposed matrix m_t of a matrix m, is the flipped matrix over its diagonal.

e.g.

    [ 1 2 3 ]           [ 1 4 7 ]
m = [ 4 5 6 ]     m_t = [ 2 5 8 ]
    [ 7 8 9 ]           [ 3 6 9 ]

e.g.

     [ 1 2 ]            [ 1 3 5 ]
m =  [ 3 4 ]      m_t = [ 2 4 6 ]
     [ 5 6 ]

Transpose? It’s just a matter of definition

Further see GLSL Programming/Vector and Matrix Operations:

Furthermore, the *-operator can be used for matrix-vector products of the corresponding dimension, e.g.:

vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2.,  3., 4.);
vec2 w = m * v; // = vec2(1. * 10. + 3. * 20., 2. * 10. + 4. * 20.)

Note that the vector has to be multiplied to the matrix from the right.

If a vector is multiplied to a matrix from the left, the result corresponds to to multiplying a column vector to the transposed matrix from the right. This corresponds to multiplying a column vector to the transposed matrix from the right:

Thus, multiplying a vector from the left to a matrix corresponds to multiplying it from the right to the transposed matrix:

vec2 v = vec2(10., 20.);
mat2 m = mat2(1., 2.,  3., 4.);
vec2 w = v * m; // = vec2(1. * 10. + 2. * 20., 3. * 10. + 4. * 20.)


This means:

If a matrix is defined like this:

mat4 m44 = mat4(
    vec4( Xx, Xy, Xz, 0.0),
    vec4( Yx, Xy, Yz, 0.0),
    vec4( Zx  Zy  Zz, 0.0),
    vec4( Tx, Ty, Tz, 1.0) );

And the matrix uniform mat4 transformation is set like this (see glUniformMatrix4fv):

glUniformMatrix4fv( .... , 1, GL_FALSE, &(m44[0][0] );

Then that the vector has to be multiplied to the matrix from the right:

gl_Position = transformation * vertexPosition;


But of course, the matrix can be set up transposed:

mat4 m44 = mat4(
    vec4(  Xx,  Yx,  Zx,  Tx),
    vec4(  Xy,  Yy,  Zy,  Ty),
    vec4(  Xz   Yz   Zz,  Tz),
    vec4( 0.0, 0.0, 0.0, 1.0) );

Or can be transposed when set to the uniform variable:

glUniformMatrix4fv( .... , 1, GL_TRUE, &(m44[0][0] );

Then that the vector has to be multiplied to the matrix from the left:

gl_Position = vertexPosition * transformation;


See further:


<hr/>

Inverse matrix

Inverse 4*4 matrix

bool InverseMat44( const GLfloat m[16], GLfloat invOut[16] )
{
    float inv[16], det;
    int i;

    inv[0]  =  m[5] * m[10] * m[15] - m[5] * m[11] * m[14] - m[9] * m[6] * m[15] + m[9] * m[7] * m[14] + m[13] * m[6] * m[11] - m[13] * m[7] * m[10];
    inv[4]  = -m[4] * m[10] * m[15] + m[4] * m[11] * m[14] + m[8] * m[6] * m[15] - m[8] * m[7] * m[14] - m[12] * m[6] * m[11] + m[12] * m[7] * m[10];
    inv[8]  =  m[4] * m[9]  * m[15] - m[4] * m[11] * m[13] - m[8] * m[5] * m[15] + m[8] * m[7] * m[13] + m[12] * m[5] * m[11] - m[12] * m[7] * m[9];
    inv[12] = -m[4] * m[9]  * m[14] + m[4] * m[10] * m[13] + m[8] * m[5] * m[14] - m[8] * m[6] * m[13] - m[12] * m[5] * m[10] + m[12] * m[6] * m[9];
    inv[1]  = -m[1] * m[10] * m[15] + m[1] * m[11] * m[14] + m[9] * m[2] * m[15] - m[9] * m[3] * m[14] - m[13] * m[2] * m[11] + m[13] * m[3] * m[10];
    inv[5]  =  m[0] * m[10] * m[15] - m[0] * m[11] * m[14] - m[8] * m[2] * m[15] + m[8] * m[3] * m[14] + m[12] * m[2] * m[11] - m[12] * m[3] * m[10];
    inv[9]  = -m[0] * m[9]  * m[15] + m[0] * m[11] * m[13] + m[8] * m[1] * m[15] - m[8] * m[3] * m[13] - m[12] * m[1] * m[11] + m[12] * m[3] * m[9];
    inv[13] =  m[0] * m[9]  * m[14] - m[0] * m[10] * m[13] - m[8] * m[1] * m[14] + m[8] * m[2] * m[13] + m[12] * m[1] * m[10] - m[12] * m[2] * m[9];
    inv[2]  =  m[1] * m[6]  * m[15] - m[1] * m[7]  * m[14] - m[5] * m[2] * m[15] + m[5] * m[3] * m[14] + m[13] * m[2] * m[7]  - m[13] * m[3] * m[6];
    inv[6]  = -m[0] * m[6]  * m[15] + m[0] * m[7]  * m[14] + m[4] * m[2] * m[15] - m[4] * m[3] * m[14] - m[12] * m[2] * m[7]  + m[12] * m[3] * m[6];
    inv[10] =  m[0] * m[5]  * m[15] - m[0] * m[7]  * m[13] - m[4] * m[1] * m[15] + m[4] * m[3] * m[13] + m[12] * m[1] * m[7]  - m[12] * m[3] * m[5];
    inv[14] = -m[0] * m[5]  * m[14] + m[0] * m[6]  * m[13] + m[4] * m[1] * m[14] - m[4] * m[2] * m[13] - m[12] * m[1] * m[6]  + m[12] * m[2] * m[5];
    inv[3]  = -m[1] * m[6]  * m[11] + m[1] * m[7]  * m[10] + m[5] * m[2] * m[11] - m[5] * m[3] * m[10] - m[9]  * m[2] * m[7]  + m[9]  * m[3] * m[6];
    inv[7]  =  m[0] * m[6]  * m[11] - m[0] * m[7]  * m[10] - m[4] * m[2] * m[11] + m[4] * m[3] * m[10] + m[8]  * m[2] * m[7]  - m[8]  * m[3] * m[6];
    inv[11] = -m[0] * m[5]  * m[11] + m[0] * m[7]  * m[9]  + m[4] * m[1] * m[11] - m[4] * m[3] * m[9]  - m[8]  * m[1] * m[7]  + m[8]  * m[3] * m[5];
    inv[15] =  m[0] * m[5]  * m[10] - m[0] * m[6]  * m[9]  - m[4] * m[1] * m[10] + m[4] * m[2] * m[9]  + m[8]  * m[1] * m[6]  - m[8]  * m[2] * m[5];

    det = m[0] * inv[0] + m[1] * inv[4] + m[2] * inv[8] + m[3] * inv[12];
    if (det == 0) return false;
    det = 1.0 / det;

    for (i = 0; i < 16; i++)
        invOut[i] = inv[i] * det;

    return true;
}

def InverseMat44(mat):
    m = [mat[i][j] for i in range(4) for j in range(4)]
    inv = [0]*16

    inv[0]  =  m[5] * m[10] * m[15] - m[5] * m[11] * m[14] - m[9] * m[6] * m[15] + m[9] * m[7] * m[14] + m[13] * m[6] * m[11] - m[13] * m[7] * m[10]
    inv[4]  = -m[4] * m[10] * m[15] + m[4] * m[11] * m[14] + m[8] * m[6] * m[15] - m[8] * m[7] * m[14] - m[12] * m[6] * m[11] + m[12] * m[7] * m[10]
    inv[8]  =  m[4] * m[9]  * m[15] - m[4] * m[11] * m[13] - m[8] * m[5] * m[15] + m[8] * m[7] * m[13] + m[12] * m[5] * m[11] - m[12] * m[7] * m[9]
    inv[12] = -m[4] * m[9]  * m[14] + m[4] * m[10] * m[13] + m[8] * m[5] * m[14] - m[8] * m[6] * m[13] - m[12] * m[5] * m[10] + m[12] * m[6] * m[9]
    inv[1]  = -m[1] * m[10] * m[15] + m[1] * m[11] * m[14] + m[9] * m[2] * m[15] - m[9] * m[3] * m[14] - m[13] * m[2] * m[11] + m[13] * m[3] * m[10]
    inv[5]  =  m[0] * m[10] * m[15] - m[0] * m[11] * m[14] - m[8] * m[2] * m[15] + m[8] * m[3] * m[14] + m[12] * m[2] * m[11] - m[12] * m[3] * m[10]
    inv[9]  = -m[0] * m[9]  * m[15] + m[0] * m[11] * m[13] + m[8] * m[1] * m[15] - m[8] * m[3] * m[13] - m[12] * m[1] * m[11] + m[12] * m[3] * m[9]
    inv[13] =  m[0] * m[9]  * m[14] - m[0] * m[10] * m[13] - m[8] * m[1] * m[14] + m[8] * m[2] * m[13] + m[12] * m[1] * m[10] - m[12] * m[2] * m[9]
    inv[2]  =  m[1] * m[6]  * m[15] - m[1] * m[7]  * m[14] - m[5] * m[2] * m[15] + m[5] * m[3] * m[14] + m[13] * m[2] * m[7]  - m[13] * m[3] * m[6]
    inv[6]  = -m[0] * m[6]  * m[15] + m[0] * m[7]  * m[14] + m[4] * m[2] * m[15] - m[4] * m[3] * m[14] - m[12] * m[2] * m[7]  + m[12] * m[3] * m[6]
    inv[10] =  m[0] * m[5]  * m[15] - m[0] * m[7]  * m[13] - m[4] * m[1] * m[15] + m[4] * m[3] * m[13] + m[12] * m[1] * m[7]  - m[12] * m[3] * m[5]
    inv[14] = -m[0] * m[5]  * m[14] + m[0] * m[6]  * m[13] + m[4] * m[1] * m[14] - m[4] * m[2] * m[13] - m[12] * m[1] * m[6]  + m[12] * m[2] * m[5]
    inv[3]  = -m[1] * m[6]  * m[11] + m[1] * m[7]  * m[10] + m[5] * m[2] * m[11] - m[5] * m[3] * m[10] - m[9]  * m[2] * m[7]  + m[9]  * m[3] * m[6]
    inv[7]  =  m[0] * m[6]  * m[11] - m[0] * m[7]  * m[10] - m[4] * m[2] * m[11] + m[4] * m[3] * m[10] + m[8]  * m[2] * m[7]  - m[8]  * m[3] * m[6]
    inv[11] = -m[0] * m[5]  * m[11] + m[0] * m[7]  * m[9]  + m[4] * m[1] * m[11] - m[4] * m[3] * m[9]  - m[8]  * m[1] * m[7]  + m[8]  * m[3] * m[5]
    inv[15] =  m[0] * m[5]  * m[10] - m[0] * m[6]  * m[9]  - m[4] * m[1] * m[10] + m[4] * m[2] * m[9]  + m[8]  * m[1] * m[6]  - m[8]  * m[2] * m[5]

    det = m[0] * inv[0] + m[1] * inv[4] + m[2] * inv[8] + m[3] * inv[12]
    for i in range(16):
        inv[i] /= det;
    return inv;


See further:


<hr/>

Inverse matrix and transposed matrix

If the transposed matrix of a matrix m is equal to the inverse matrix of the matrix m, it is called an orthogonal matrix.

This means, if each column of a amtrix (e.g. each axis of a 3*3 matrix), has unit length and is perpendicular to every other column then the transposed matrix is equal the inverse matrix.

e.g.

    [  0.707, 0.707, 0 ]                 [ 0.707, -0.707, 0 ]
m = [ -0.707, 0.707, 0 ]     m_i = m_t = [ 0.707,  0.707, 0 ]
    [      0,     0, 1 ]                 [     0,      0, 1 ]


See further:


<hr/>

Normal vector transformation

If a normal matrix has to be created form a 44 matrix, then the inverse transposed of the upper left 33, of the 4*4 matrix has to be calculated.

mat4 m44; mat3 normal_m33 = transpose(inverse(mat3(m44)));

vec3 v; vec3 v_ = normal_m33 * v;

See:


Since, if a vector is multiplied to a matrix from the left, the result corresponds to to multiplying a column vector to the transposed matrix from the right, this can be simplified and the transpose operation can be avoided:

    vec3 v_ = v * inverse(mat3(m44)); 
``

<br/>
If the 4*4 matrix `transformationMatrix` is a [Orthogonal matrix](https://en.wikipedia.org/wiki/Orthogonal_matrix), this means the X, Y, and Z axis are [Orthonormal](https://en.wikipedia.org/wiki/Orthonormality) (unit vectors and they are normal to each other), then it is sufficient to use the the upper left 3*3. In this case the inverse matrix is equal the transposed matrix.

See [In which cases is the inverse matrix equal to the transpose?](https://math.stackexchange.com/questions/156735/in-which-cases-is-the-inverse-matrix-equal-to-the-transpose)

```glsl
vec3 v_ = mat3(m44) * v;


See further:


<hr/>

Combined transformations

Let’s assume we have an object that is moved, rotated and scaled, and we define a transformation matrix as follows:

glm::mat4 objTrans ...; // translation
glm::mat4 objRot ...;   // rotation
glm::mat4 objScale ...; // scaling

glm::mat4 objMat = objTrans * objRot * objScale;

And we have rotation matrix that we want to run on the object. In this case we have rotation around the Z-axis:

foat angle ...; // rotation angle

glm::mat4 rotMat = glm::rotate( angle, glm::vec3( 0.0, 0.0, 1.0 ) );

We have several rotations we can do with this information. First we want to rotate the object on its local axis:

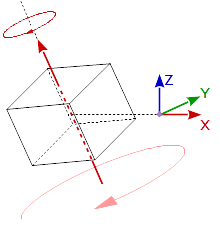
rotate local axis

glm::mat4 modelMat = objMat * rotMat;

A Rotation around the worlds origin can be performed like this:

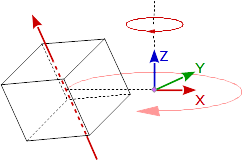
rotate world origin

glm::mat4 modelMat = rotMat * objMat;

In order to rotate around the origin of the object in the world coordinate system, we must eliminate the rotation of the objct:

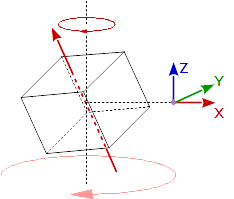
rotate object origin

glm::mat4 modelMat = objMat * (glm::inverse(objRot) * rotMat * objRot);

A Rotation around the worlds origin in relation to the object you have to do the opposite:

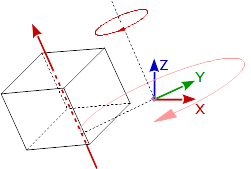
rotate object world

glm::mat4 modelMat = (objRot * rotMat * glm::inverse(objRot)) * objMat;

If you have a complete transformations matrix for an object and you do not know the rotation part, then it can be easily determined.

Note that a transformation matrix usually looks like this:

( X-axis.x, X-axis.y, X-axis.z, 0 )
( Y-axis.x, Y-axis.y, Y-axis.z, 0 )
( Z-axis.x, Z-axis.y, Z-axis.z, 0 )
( trans.x,  trans.y,  trans.z,  1 )

To generate a rotation only matrix you have to extract the normalized axis vectors:

glm::mat4 a ...; // any matrix
glm::vec3 x = glm::normalize( a[0][0], a[0][1], a[0][2] );
glm::vec3 y = glm::normalize( a[1][0], a[1][1], a[1][2] );
glm::vec3 z = glm::normalize( a[2][0], a[2][1], a[2][2] );

glm::mat4 r;
r[0][0] = x[0]; r[0][1] = x[1]; r[0][2] = x[2]; r[0][3] = 0.0f;
r[1][0] = y[0]; r[1][1] = y[1]; r[1][2] = y[2]; r[0][3] = 0.0f;
r[2][0] = z[0]; r[2][1] = z[1]; r[2][2] = z[2]; r[0][3] = 0.0f;
r[3][0] = 0.0f; r[3][1] = 0.0f; r[3][2] = 0.0f; r[0][3] = 1.0f;


See further:


<hr/>

First Person Camera Transformation

For the controlled movement of an object through the scene, the matrix which specified the position and the orientation has to be incrementally changed. This means you have to calculate the current movement and current rotation matrix. Apply the movement and rotation to the position matrix and store the model matrix for the next frame. At the next frame you have to use the manipulated position matrix from the previous frame and you have to apply the new movement and rotation. This causes that the position and orientation incremental changes, always based on its current position and orientation.

movement and rotation


See further:


<hr/>

profile for Rabbid76 on Stack Exchange, a network of free, community-driven Q&A sites