graphics-snippets

---

• Intersection
  • Intersection of 2 lines (2 dimensional)
  • Intersection of a line and a plane
    • Intersection of the Line of Sight and the Viewport

Intersection

<hr/>

Intersection of 2 lines (2 dimensional)

Related questions

• Intersect a ray with a triangle in GLSL C++

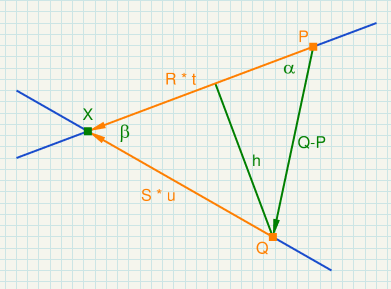
P     ... point on the 1. line
R     ... direction vector of the 1. line

Q     ... point on the 2. line
S     ... direction vector of the 2. line

alpha ... angle between Q-P and R
beta  ... angle between R and S

X     ... intersection point
t     ... distance between P and X
u     ... distance between Q and X

gamma  =  180° - alpha - beta

t  = | Q - P | * sin(gamma) / sin(beta)
u  = | Q - P | * sin(alpha) / sin(beta)

t  =  dot(Q-P, (S.y, -S.x)) / dot(R, (S.y, -S.x))  =  determinant(mat2(Q-P, S)) / determinant(mat2(R, S))
u  =  dot(Q-P, (R.y, -R.x)) / dot(R, (S.y, -S.x))  =  determinant(mat2(Q-P, R)) / determinant(mat2(R, S))

X  =  P + R * t  =  Q + S * u

<hr/>

Intersection of a line and a plane

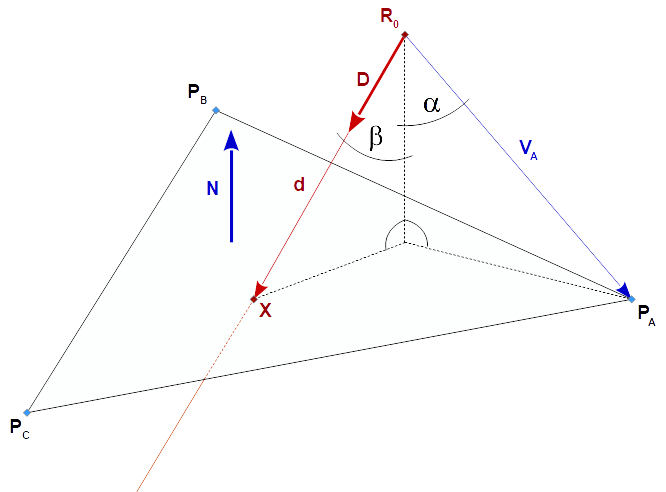
The ray is defined by a point R0 and a direction D.
The plane is defined by a triangle with the three points PA, PB, and PC.

The normal vector of the plane can be calculated by the cross product of 2 legs of the triangle:

N  =  cross(PC-PA, PB-PA)

The normal distance n of the point R0 to the plane is:

n  =  | R0 - PA | * cos(alpha)  =  dot(PA - R0, N)

It follows that the distance d of the intersection point X to the origin of the ray R0 is:

d  =  n / cos(beta)  =  n / dot(D, N)

The intersection point X is:

X  =  R0 + D * d  =  R0 + D * dot(PA - R0, N) / dot(D, N)

Intersection of the Line of Sight and the Viewport

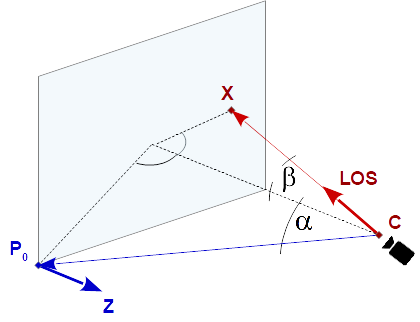
P0  ... any known point on the viewport
Z   ... Z-axis of the viewport 
C   ... camera position
LOS ... line of sight

X  =  C + LOS * dot(P0 - C, Z) / dot(LOS, Z)

---